Scorers
What is a scorer?
A scorer calculates how well some target group matches with some collected targeting data. It produces a score between 0 and 1 (inclusive).
A scorer is tied to a characteristic, and can compute a score of the targeted data of a visitor for some characteristic. See the example of Scoring and Normalization again where we had:
RawScore['Urban Sunbather', V] := Value['Amsterdam', V] * Value['Sunny', V]
whereValue['Amsterdam', V] is the score of visitor V on whether he comes from Amsterdam or not, and Value['Sunny', V] whether it is sunny for visitor V. These values are computed by the scorers of the 'comes from (city)' and 'experiences (weather)' characteristic.
Types of scorers
In general, a scorers can be booleanor fuzzy.
Boolean scorers
A boolean scorer returns either 0 or 1, and nothing in between (similar to true or false). Such scorers typically belong to characteristics like:
-
Is the visitor logged in?
-
Does the visitor come from the US?
-
Does the visitor come from a big city?
-
Is it Tuesday today?
The scorers for the characteristic above either return 0 or 1 as a score, since anything in between is not a sensible result.
Fuzzy scorers
A fuzzy scorer can return a score between 0 and 1 (including 0 and 1 itself). Fuzzy scorers typically belong to characteristics like:
-
Mostly looked at documents tagged as...
-
Mostly looked at documents of type...
-
Mostly searched with terms ...
-
Is a loyal visitor ...
Developers can implement their own fuzzy scorers.
Segment score calculation example: expensive cars
Assume we want to have a segment 'Expensive car seeker' to target visitors that mostly look at documents that are tagged as 'expensive cars'. For this segment we will use:
-
The characteristic 'mostly looks at documents that are tagged as (tags)'
-
The target group 'expensive cars'
In our example, documents that represent expensive cars are tagged differently than documents that represent cheap cars. Hence we can (fuzzily) identify someone mostly looking at expensive cars by collecting the tags of the visited documents. Assume that we, marketers, have identified the segment 'Expensive car seeker' as someone who mostly looks at car documents with tags 'sports wagon, high quality, fast, expensive'. The score of the visitor V we would like to target now becomes:
RawScore['Expensive car seeker', V] := Value['sports wagon, high quality, fast, expensive', V]
You can combine the above with other scored characteristics (boolean or fuzzy). For example, we could also calculate the score for a segment 'Expensive car seeker from the US' as follows:
RawScore['Expensive car seeker from US', V] := Value['sports wagon, high quality, fast, expensive', V] * Value['US', V]
From the Expensive car seeker from the US segment rule above, it makes sense that:
-
Value['US', V] either returns 0 or 1 and nothing in between
-
Value['sportswagon, high quality, fast, expensive', V] might return 0 or 1, but also something close to 1 for a visitor that looked mostly at expensive tagged car documents, but also a few not so expensive ones.
Note that the fuzzy VectorScoringEngine (explained below) can also use a weight per term by adding a frequency as value in the target group configuration. For example, when the tag 'expensive' is more important than 'sportswagon', which in turn is more important than the others, the target group can be something like:
Value['sportswagon * 3 , high quality, fast, expensive * 10', V]
The fuzzy Vector Scorers
The Relevance Module already ships with a fuzzy scorer that is used by some standard characteristics (like 'mostly looks at documents of type' or 'mostly looks at documents tagged with', or 'mostly searches with') already. It is called the Vector Scorer, and is quite generally applicable to fuzzy scores. It resembles the way that general search libraries like Lucene implement 'more like this' (see for example Similarity), except for the inverse document frequencies part. We don't need that as this is covered by Scoring and Normalization and works on actual visitors instead of documents.
Score calculation
The vector scorer takes two arrays of terms (term vectors), normalizes these arrays to a length of 1 (Euclidean length), and computes the dot product of these term vectors (i.e. the cosine of the angle between the two term vectors). Thus, the score (cosine similarity of their vector representations 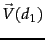 and
and 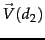 ) of two term vectors d1 and d2 is:
) of two term vectors d1 and d2 is:
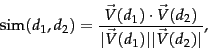
Please note the following parts:
-
The normalization to vectors of length 1 is to assure that vectors which point in the exact same direction, but are of unequal length, still score 1.
-
The scoring similarity in this way the relative ordering of terms is lost : It does not matter in which order the terms in the vector occur.
-
All terms are weighted equally when equal frequency. Boosting a term to be more important can be done by raising the frequency.
Example
Assume that a visitor A visited documents with the following tags:
-
2 times expensive
-
2 times sportswagon
-
1 times luxury
-
1 time fast
The collector of the characteristic 'mostly looks at documents that are tagged as (tags)' will have collected these tags in the targeting data of visitor A.
These collected tags can now be seen as a four-dimensional vector going 2 times along the expensive axis, 2 times the sportswagon, 1 times....etc. Also, this visitor scores most likely pretty OK against the RawScore['Expensive car seeker', V] because the expensive car seeker contained the target group Value['sportswagon, high quality, fast, expensive', V.
Now, also assume a visitor B that is more cheap car minded, but still wants a fast and fancy looking car. For this visitor the following tags have been collected:
-
2 times fast
-
3 times cheap
-
1 time Italian
If we compute the score for visitor A and B we get:
Visitor A:
RawScore['Expensive car seeker', Visitor A] := [2 x 1 + 2 x 1 + 1 x 0 + 1 x 1] / [ sqrt(2^2 + 2^2 + 1^2 + 1^2) x sqrt(1^1 + 1^1 + 1^1 + 1^1) ] = 5 / 6.32 = 0.79
Visitor B:
RawScore['Expensive car seeker', Visitor B] := [2 x 1 + 3 x 0 + 1 x 0] / [ sqrt(2^2 + 3^2 + 1^2) x sqrt(1^1 + 1^1 + 1^1 + 1^1) ] = 2 / 7.48 = 0.27
As you can see, visitor A scores much better than visitor B against target group mostly looks at documents that are tagged as 'expensive cars'.
References
Further suggested readings:
-
Dot product http://nlp.stanford.edu/IR-book/html/htmledition/dot-products-1.html
-
Lucene similarity http://lucene.apache.org/core/old_versioned_docs/versions/2_9_0/api/all/org/apache/lucene/search/Similarity.html

